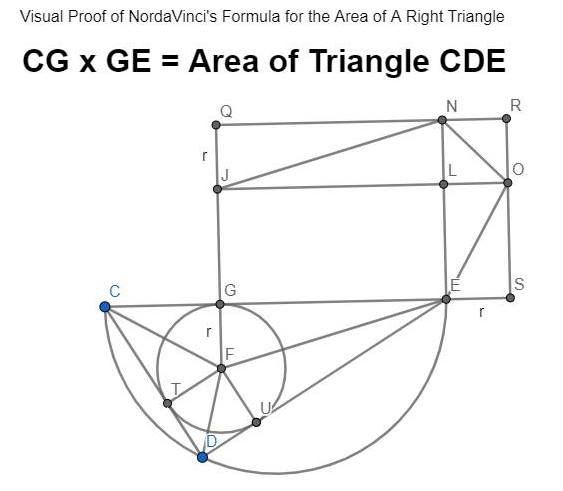
After studying Euclid’s Elements for a day or two, I realized how, 2400 years ago, they might have approached the proof of what I have taken the liberty of calling NordaVinci’s Formula for the Area of a Right Triangle – until if and when the rightful owner of this formula emerges as someone in history who noticed it before I did, which is becoming harder and harder to believe that there wasn’t at least someone in the last 2400 or more years.

Looking at the famous Proposition 47 of Book I of Euclid, which is basically the proof of the Pythagorean Theorem, I realized that it’s very simple, once one asks the question to realize that R(H + R) = X(H – X) would be immediately recognized 2,400 years ago as the dimensions of two rectangles whose areas are equal but with differently proportioned sides. R being the radius of the inscribed circle, H being the hypotenuse and X and H- X being the segments of the hypotenuse from the tangent point to the hypotenuse of the inscribed circle.

By cutting out the 6 inner right triangles and rearranging them around the rectangle formed by the two segments of the hypotenuse, a second bigger rectangle is formed whose edges are equal to the two legs of the bigger right triangle, the product of which is twice the area of the bigger right triangle. Thus it simply must be that the product of the two segments of the hypotenuse also equal the area of the bigger right triangle.