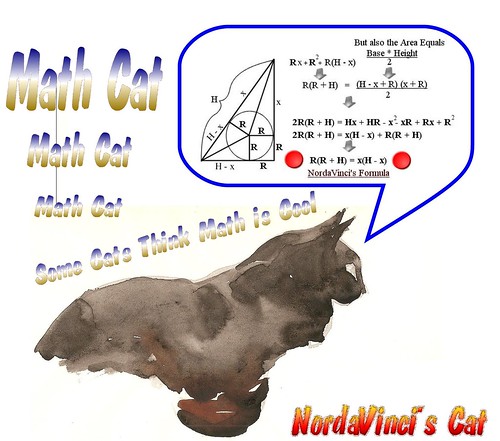
By the way, I discovered a new, previously completely unknown formula for the area of a right triangle. I call it “NordaVinci’s Formula.” Here it is R(R + H) = X(H – X). Here’s a link to my “NordaVinci’s Cat” poster with the Cat thinking about the derivation of NordaVinci’s Formula, that you can purchase for $20 – the poster, not the Cat. Be one of the first in the world to know something about the Right Triangle that is not in the Elements of Euclid Math Book or any other Math Book in Human History! Be one of the first to be able to brag to your trigonometry teacher that you know something that he or she doesn’t know about the area of a right triangle! Sell the poster to your teacher for only $30. Profits are for a non-profit group involving math, science and technology!
NordaVinci’s Formula is not simpler. That’s what kept it hidden for these many thousands of years – nobody cared, nobody needed to know it, and there was a simpler formula.
The interesting thing is that when I began to investigate, thinking that this must be common knowledge and I can’t imagine that I am the first person in recorded human history to notice this, I went to mathworld online reference and noticed in the footnotes the mention of Baker from 1884 who had collected a list of 130 different formulas for the area of a triangle, none of which is NordaVinci’s Formula.
REFERENCES:
Baker, M. “A Collection of Formulæ for the Area of a Plane Triangle.” Ann. Math. 1, 134-138, 1884.
I sent questions to some experts who didn’t bother to respond as of yet, and unless I pay somebody a few thousand dollars to do a literature search of extant scholarly journals, I won’t know if anyone in the world today ever wrote about this as something that was already discovered.
The brief point of NordaVinci’s Formula that was unknown is the right side of the equation. The left side was known already and easy to see from the diagram. The right side is simply X(H-X), which was unknown as the Area of a Right Triangle. That means that the tangent point of the inscribed circle to the hypotenuse, divides the hypotenuse into two line segments, of which the product of their lengths equals the area of the triangle.
That’s the actual contribution to the History of Trigonometry, that was lurking there just waiting to be discovered, waving its hand in the air, shouting, “Here I am!!!”
But nobody until me noticed it, apparently.
List of Triangle Area Formulas
https://drive.google.com/open?id=1U6r0nRddrHuxf_tglbg0fB7FLaCpK9I_
LikeLike
List of Triangle Area Formulas (Continued)
https://drive.google.com/open?id=1K5n0rNMDcdyOsIbUlL0Zczx5BFUY08DP
LikeLike
For those interested, notice that formula #73 is “sr” where “s” = 1/2 of the perimeter, known as the “semiperimeter.” For a right triangle drawn and labeled as in my “NordaVinci’s Cat” poster, the “semiperimeter” is the same as “H + R.” Thus the “sr” formula is the same as my formula R(R+H), which I said was obvious and previously known.
Since I arrived at “NordaVinci’s Formula” for the area of a right triangle, by equating two known formulas and reducing to R(R+H) = x(H-x), this is of course not rocket science, but, it is interesting that it’s not common knowledge, and thus, until somebody shows otherwise, I am still claiming the right to name it as “NordaVinci’s Formula for the Area of a RIght Triangle.”
REFERENCES:
Baker, M. “A Collection of Formulæ for the Area of a Plane Triangle.” Ann. Math. Vol. 1 No. 6 (Jan. 1885), 134-138, 1884 continued in Ann. Math. Vol. 2 No. 1 (Sep., 1885) pp. 11-18
LikeLike
Very important reference, whom I wrote to, Clark Kimberling, but who has not responded as of yet.
https://en.wikipedia.org/wiki/Encyclopedia_of_Triangle_Centers
LikeLike
Related from Clark Kimberling’s info
https://faculty.evansville.edu/ck6/encyclopedia/ETC.html
LikeLike
Also interesting math hobby site
https://www.chrisvantienhoven.nl/mathematics/encyclopedia-of-poly-geometry
LikeLike
Is there another formula for the area of a triangle that reduces to X(H-X) for a right triangle?
LikeLike
The hypotenuse of any right triangle is actually the diameter of the circumscribed circle, meaning that of course the two line segments created by dividing the hypotenuse at the point of tangency to the inscribed circle, always add up to the hypotenuse or diameter of the circumscribed circle.
LikeLike
LikeLike